Объемная модель планирования. «Модель кристалла».
Объемная модель планирования. «Модель кристалла».
В данной статье автор излагает свои предположения относительно того, как в будущем будут строится модели планирования. Автор предпринял попытку предложить систему планирования, легко поддающуюся автоматизации и позволяющую отслеживать значительное количество параметров прохождения проектов, а также видеть их взаимосвязи.

Абсолютное большинство компаний в целях планирования мероприятий и проектов использует двухмерную систему планирования, берующую свое начало от знаменитой диаграммы Ганта. Первый формат диаграммы был разработан Генри Л. Гантом в 1910 году. По сути, диаграмма Ганта состоит из полос, ориентированных вдоль оси времени. Каждая полоса на диаграмме представляет отдельную задачу в составе проекта (вид работы), её концы — моменты начала и завершения работы, её протяженность — длительность работы. Вертикальной осью диаграммы служит перечень задач. Кроме того, на диаграмме могут быть отмечены совокупные задачи, проценты завершения, указатели последовательности и зависимости работ, метки ключевых моментов (вехи), метка текущего момента времени «Cегодня» и др.
Ключевым понятием диаграммы Ганта является «Веха» — метка значимого момента в ходе выполнения работ, общая граница двух или более задач. Вехи позволяют наглядно отобразить необходимость синхронизации, последовательности в выполнении различных работ. Вехи, как и другие границы на диаграмме, не являются календарными датами. Сдвиг вехи приводит к сдвигу всего проекта. Поэтому диаграмма Ганта не является, строго говоря, графиком работ. И это один из основных её недостатков. Кроме того, диаграмма Ганта не отображает значимости или ресурсоемкости работ, не отображает сущности работ (области действия). Для крупных проектов диаграмма Ганта становится чрезмерно тяжеловесной и теряет всякую наглядность.
Указанные выше недостатки и ограничения серьёзно ограничивают область применения диаграммы. Тем не менее, в настоящее время диаграмма Ганта является стандартом де-факто в теории и практике управления проектами, по крайней мере, для отображения Структуры перечня работ по проекту.
Кроме того, используя диаграмму Ганта, трудно показать распределение работ по функциональным единицам в компании (по сотрудникам или отделам), форма диаграммы не дает информации о проекте в целом, что затрудняет принятие управленческих решений руководством. Также по форме диараммы Ганта невозможно классифицировать проекты и делать экспресс-оценку прохождению проекта в целом. Диаграмма позволяет проводить выборку лишь по ограниченному числу критериев.

Также стоит отметить, что в эпоху развития информационных технологий диаграмма Ганта, не претерпевшая серьезных изменений за свою столетнюю историю, продолжает оставаться довольно архаичной структурой, слабо поддающейся автоматизации. Так, наиболее известная в мире версия программы, созданной на основе диаграммы Ганта – это программа Microsoft Project (или MSP) — программа управления проектами, разработанная и продаваемая корпорацией Microsoft. Microsoft Project создаёт расписания критического пути. В основе метода лежит определение наиболее длительной последовательности задач от начала проекта до его окончания с учетом их взаимосвязи. Задачи, лежащие на критическом пути (критические задачи), имеют нулевой резерв времени выполнения, и, в случае изменения их длительности, изменяются сроки всего проекта. В связи с этим, при выполнении проекта критические задачи требуют более тщательного контроля, в частности, своевременного выявления проблем и рисков, влияющих на сроки их выполнения и, следовательно, на сроки выполнения проекта в целом. В процессе выполнения проекта критический путь проекта может меняться, так как при изменении длительности задач некоторые из них могут оказаться на критическом пути.
При этом инструментами корректировки критического пути являются инструменты общего или производственного менеджмента, сама модель не дает требуемых подсказок руководителю, она лишь констатирует факт. К диаграмме трудно применить подходы математического моделирования, не реально использовать возможности современной компьютерной графики для визуализации модели, дающей дополнительные возможности для принятия решения при работе с моделью.

Также, при внимательном рассмотрении моделей планирования процессов, стоит обратить внимание на законы развития технических систем (ЗРТС), разработанные Г.С Альтшуллером и его последователями в области знаний, называемой «теория решения изобретательских задач – ТРИЗ». На первый взгляд может показаться, что ЗРТС здесь не причем, они предназначены для описания процесса эволюции технических систем. Но в том-то и дело, что сама по себе эволюция – уже процесс, а значит ЗРТС – это прежде всего, средство описания процессов. Известно также предположение о схожести процессов, происходящих в мире, говорящее о том, что законы, работающие в одной части мира, обычно работают и в другой его части, но с некоторыми ограничениями и особенностями. В любом случае, важность ЗРТС в том, что они не просто констатируют факт, а подсказывают направление наиболее эффективных изменений, дают возможность осуществлять долгосрочное прогнозирование, и что самое главное – подсказывают разработчику следующий шаг в развитии систем.
Ниже приведен перечень основных ЗРТС (Альтшуллер Г.С. «О законах развития технических систем», 20.01.1977 г., развернутые в более поздних работах учеников Г.С. Альтшуллера):
1. Закон полноты частей технической системы;
2. Закон энергетической проводимости технической системы;
3. Закон согласования ритмики частей системы;
4. Закон увеличения степени идеальности;
5. Закон неравномерности развития частей системы;
6. Закон перехода в надсистему;
7. Закон перехода с макро-уровня на микро-уровень
8. Закон повышения степени вепольности.
Позже к законам развития технических систем был добавлен закон эволюции систем по S-образной кривой, некоторые законы претерпели изменения формулировок (закон согласования-рассогласования частей системы, закон развертывания свертывания систем). Методики прогнозирования на основе ЗРТС разработаны такими авторами как Б. Злотин, А. Зусман, С. Литвин, В. Герасимов, Ю. Саламатов и др.
Встает вопрос – какую выбрать модель, если диаграмма Ганта оказалась столь удачной, что не претерпела существенных изменений за вековую историю? На помощь приходит все та же теория эволюции технических систем – переход от линии (последовательность выполнения операций на временном отрезке) к плоской системе координат (диаграмма Ганта), от плоской модели – к объемной. Так что объемная модель планирования процессов – вполне закономерный логический переход, отражение законов развития систем. Значит, для осуществления следующего шага нужно не совершенствовать двухмерную модель, а переходить в трехмерное измерение. Разумеется, выполнять планирование с использованием подобных моделей, имея перед собой карандаш и лист бумаги не представляется возможным. Поэтому, подобная система планирования вряд ли прижилась бы лет 20 назад. Однако сегодня, с использованием современных средств визуализации, подобная система может оказать существенную пользу при разработке проектов, о чем уже упоминалось выше. Кроме того, подобная модель – ни что иное, как полисистема, состоящая из множества плоскостей (бисистем). Поэтому, при создании компьютерной программы на основе данной модели, несомненно потребуется предусмотреть возможность вычленять различные бисистемы (плоскости) и моносистемы (линии), несущие различную функциональную нагрузку.
В этом случае, появляется возможность экспресс-анализа полисистемы (объемной модели) в целом и детализированного анализа процессов по плоскостям и даже отрезкам. То же можно говорить о вводе исходных данных: данные могут вводятся в таблицы, представляющие не что иное, как плоскости (бисистемы) и отрезки (моносистемы), а затем компьютерная программа строит полисистему – объемную модель.
Что должно лечь в основу объемной модели планирования? Разумеется законы, по которым развиваются процессы. Сразу оговоримся: в данном случае речь не идет о процессах, протекающих независимо от субъекта изменений. Речь идет о процессах, сознательно инициируемых субъектом и имеющих конечную цель, например, таких процессах, как строительство дома или технико-коммерческая проработка крупного клиента (по сути, речь идет о проектах). Подобные процессы всегда имеют начальную точку и конечную точку, то есть, сначала развертываются, а затем свертываются (процесс постепенно развивается, затягивая все большее количество субъектов, затем, по мере приближения к цели проекта, количество субъектов, участвовавших в нем, снижается. С другой стороны, если рассматривать изменение задач, то картина повторится – в начале задач будет мало, затем, по мере развития проекта, их количество возрастет и, по мере приближения к завершению проекта, снова уменьшится). Таким образом, развитие проекта подчиняется закону развертывания-свертывания систем, причем, как по субъектам, так и по выполняемым задачам. Заметим, что в диаграмме Ганта, представляющим собой бисистему с координатами время – выполняемые задачи, наглядно представлен лишь процесс развертывания-свертывания проекта по выполняемым задачам. Анализ развертывания-свертывания проекта по субъектам или квалификации персонала по диаграмме Ганта сильно затруднен.
Если же представить процесс развертывания и свертывания проекта в виде объемной модели, мы получим не что иное, как модель кристалла с вершинами на временной оси, где:
А – начало проекта; В – завершение проекта, то получим такое вот изображение:
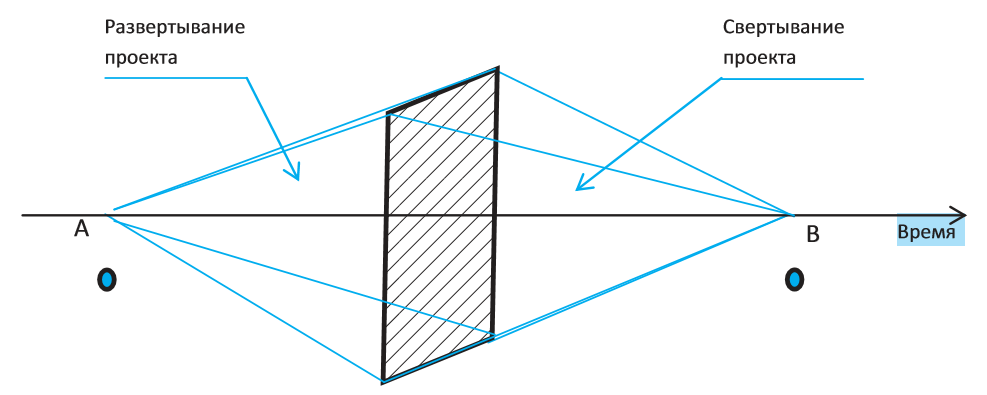
Рис. 1. Образная модель кристалла, описывающая процесс планирования.
Однако в таком виде модель, хоть и наглядна, но представляет сложности с ее описанием и последующим анализом, поэтому преобразуем модель кристалла в несколько иной вид, удобный для ввода исходных данных и последующего анализа.
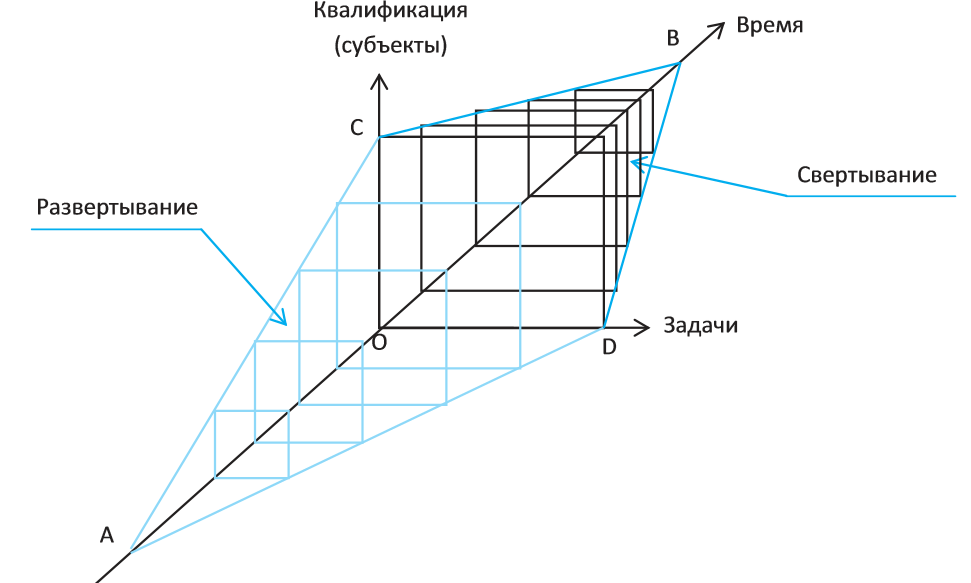
Рис.2. Преобразованная модель кристалла.
Анализируя модель кристалла, можно выделить несколько функциональных плоскостей (таблиц). Основных плоскости 3:
1) Плоскость AOBD, по сути представляет собой диаграмму Ганта. Анализируя эту плоскость, можно получить картину развертывания — свертывания задач по времени, вычислять параметры критического пути, рассматривать варианты распараллеливания процессов во времени, то есть в этой плоскости доступны стандартные операции, принятые в диаграмме Ганта. Диаграмма Ганта входит в данную модель в качестве подсистемы, модель кристалла – это модель планирования более высокого уровня, что опять же подтверждает правильность выбранной модели в соответствии с законами развития систем, а именно, с законом перехода в надсистему (модель не упраздняет прекрасно проработанный существующий инструмент планирования, а включает его в свой состав в качестве подсистемы).
2) Плоскость AOBС представляет собой картину развертывания — свертывания процессов по субъектам, задействованным в решении задач. Анализ этой поверхности позволяет получить картину изменения во времени требуемой квалификации или загрузку субъектов, участвующих в процессе. Таким образом, если проектов несколько, то можно построить не один кристалл, а систему кристаллов и путем взаимного расположения моделей добиваться того, чтобы загрузка каждого субъекта была сбалансирована (рис. 3).
3) Плоскость СOD показывает зависимость выполняемых задач от квалификации субъекта. Анализируя данную плоскость. Можно установить максимальную сложность задач и максимально требуемую квалификацию субъекта, требуемую для ее выполнения. Фактически, плоскость COD представляет собой таблицу, позволяющую установить, какой субъект используется для решения каких задач – можно ли гарантировать, что квалификация субъекта достаточна, или что наоборот, в данной компании предпочитают «микроскопами гвозди забивать». Анализируя срез по этой плоскости, можно накопить достаточную статистику для корректировки должностных инструкций, что также весьма ценно. Кроме того, поскольку данный срез можно проводить в определенные промежутки времени, то есть, назначать на шкале времени контрольные точки (см. плоскости, параллельные плоскости COD), то можно получить информацию об изменении во времени квалификации персонала и сложности решаемых задач, а также исключить нерациональное использование субъектов в будущем.
В данной модели, помимо плоскостей (бисистем), важнейшими понятиями являются моносистемы – векторы, главные из которых – это вектор субъектов и вектор задач. Вектор субъектов и вектор задач проходят параллельно оси времени, принадлежат соответственно плоскостям АОВС и AOBD и показывают начало и конец выполнения задачи, а также начало и конец загрузки субъекта в данном проекте. Понятие «вектор задач» соответствует линии задач в диаграмме Ганта.
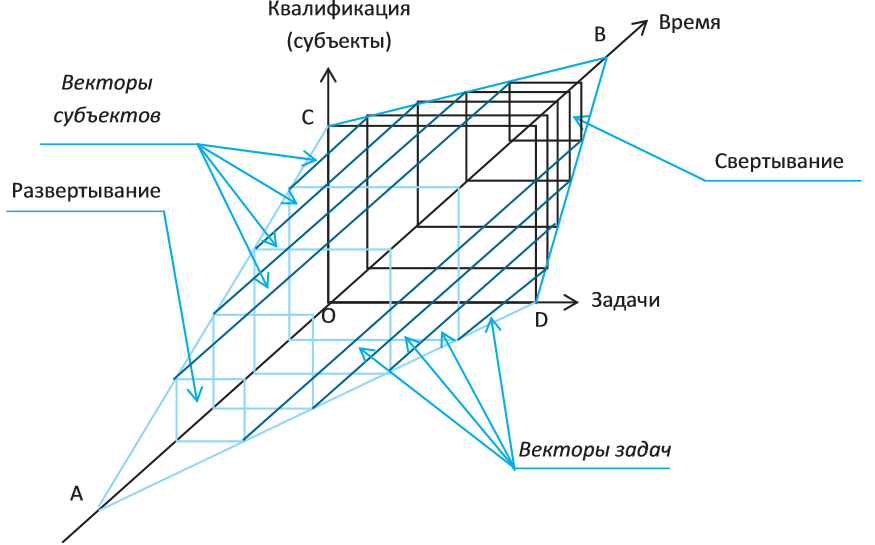
Рис.3. Векторы субъектов и векторы задач в модели кристалла.
По длине векторов субъектов легко судить о загрузке субъектов в определенные периоды времени. При необходимости можно сделать срезы по субъектам в определенные моменты времени и рассмотреть плоскость СOD, на которой вектора субъектов будут представлены в виде точечной диаграммы, удобной для анализа в данный момент времени.
По длине векторов задач легко судить о выполнении задач в данный период времени, то есть проводить анализ, аналогичный анализу по диаграмме Ганта. При необходимости можно сделать срезы по задачам в определенные моменты времени и рассмотреть плоскость СOD, на которой вектора субъектов будут представлены в виде точечной диаграммы, удобной для анализа в данный момент времени.
Как уже становится понятно, плоскость СOD показывает не только срез по задачам и субъектам в определенный момент времени, но и позволяет построить линейчатую диаграмму, показывающую корреляцию между субъектами и выполняемыми ими задачами. При необходимости, на экран монитора можно будет вывести плоскости, показывающие данную корреляцию, но уже привязанную ко времени. Таким образом, мы можем получить картину как мгновенной корреляции задач и субъектов, так и посмотреть изменение картины во времени. С точки зрения законов развития систем, подобная корреляция – не что иное, как отражение закона согласования-рассогласования частей системы, который показывает, в каком месте системы требуется вмешательство с целью корректировки процесса. Постараюсь продемонстрировать сказанное на рисунках.
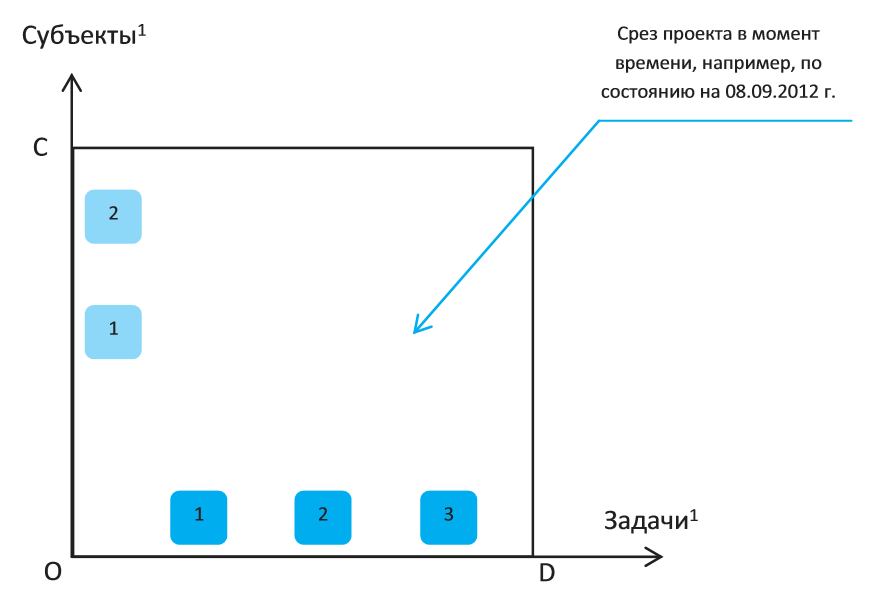
Рис. 4. Точечная диаграмма, показывающая наличие задач в определенный промежуток времени и субъекты, задействованные в процессе их выполнения.
*Прим.: субъекты располагаются на координатной оси в зависимости от квалификации, задачи – в зависимости от сложности. Чем выше сложность задачи и чем выше квалификация субъекта, тем выше их положение на координатной оси.
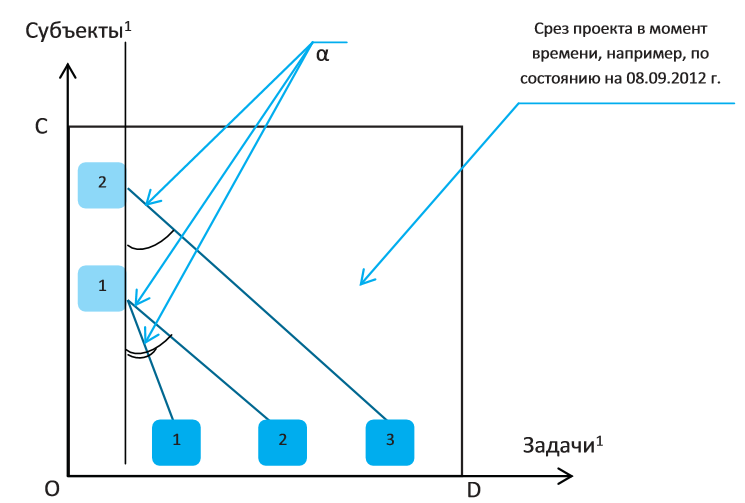
Рис. 5. Линейчатая диаграмма, показывающая согласование-рассогласование сложности выполняемых задач в определенный промежуток времени с квалификацией субъектов, задействованных в процессе их выполнения.
Анализируя ситуацию, изображенную на рис. 5, можно по углу наклона красной линии α судить о согласовании либо рассогласовании требуемой квалификации субъекта со сложностью выполняемый задачи в данный момент времени. Например, если угол α слишком мал (крутой склон), то квалификация субъекта явно больше, чем того требует сложность поставленной задачи – ресурс используется неэффективно. Если угол α слишком велик (пологий склон), то субъекту наверняка поставлена задача, которая ему «не по зубам» и вряд ли стоит ждать качественного ее выполнения. Кроме того, диаграмма четко показывает загрузку каждого субъекта в данный момент времени – об этом можно судить по числу красных линий, показывающих связь выполняемой задачи с субъектом, отвечающим за ее выполнение.
Кроме того, как указывалось выше, модель позволяет проанализировать корреляцию уровня квалификации объекта со сложностью выполняемых задач не только в определенный момент времени, но и на определенном временном промежутке. Этот анализ можно выполнить, если рассмотреть плоскость, образованную вектором субъектов и вектором задач (или поверхность, так как в реальной модели вектора, а следовательно, и поверхности, не обязательно будут линейными). Проводя анализ данной поверхности, можно учитывать угол наклона поверхности к оси ОС или OD, ширину поверхности и ее длину, а также ее кривизну. Данный анализ представлен на рис. 6.
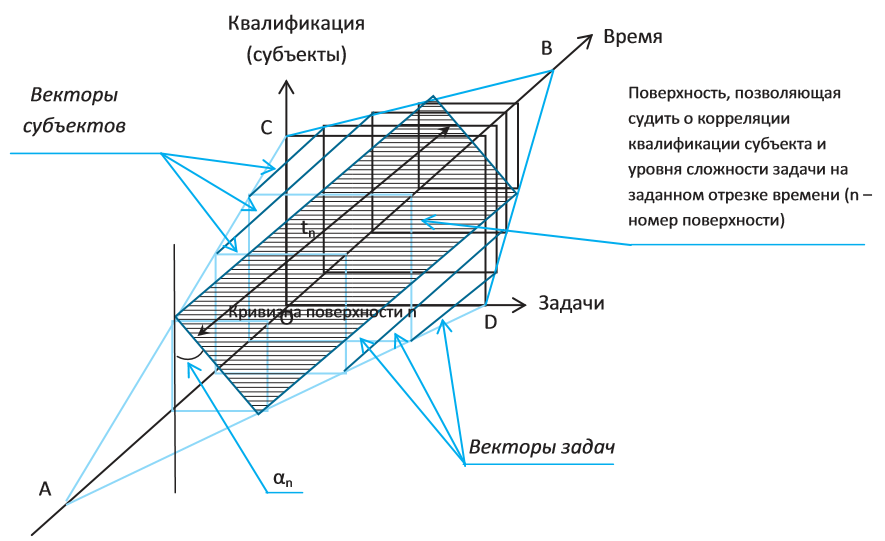
Рис. 6. Поверхности, образованные векторами субъектов и векторами задач.
Представляется возможным также строить системы, состоящие из нескольких кристаллов. В подобную полисистему объемная модель кристалла входит в качестве одной из подсистем. В этом случае каждый кристалл описывает один проект, при этом векторы субъектов и векторы задач принадлежат нескольким кристаллам.
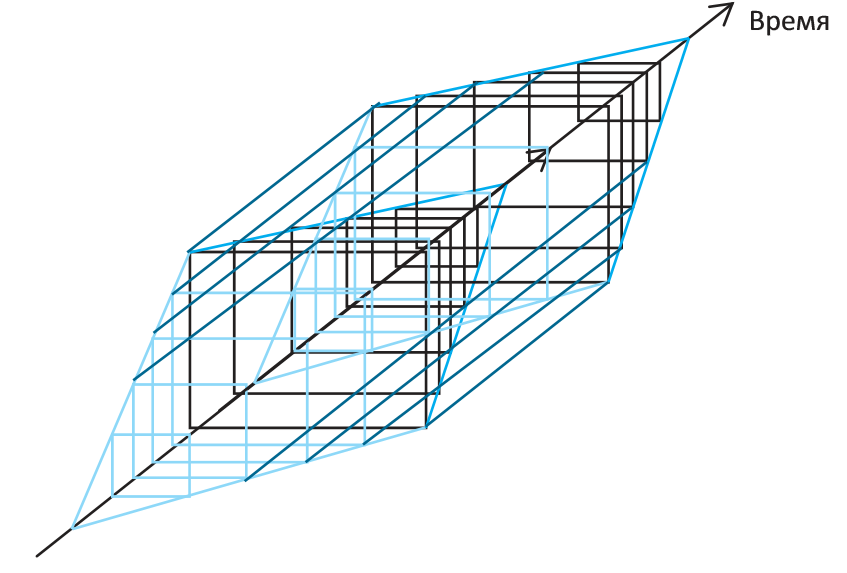
Рис. 7. Полисистема, состоящая из нескольких объемных моделей кристаллов, объединенных векторами субъектов и векторами задач.
Напоследок стоит добавить, что анализу могут подвергаться не только векторы, плоскости и поверхности, но и внешний вид модели кристалла. Дело в том, что в своей статье я представил идеализированную модель, которая везде изображена в виде «правильного кристалла» без искривлений формы. На практике поверхность кристалла может принимать самые разнообразные формы, иметь «выпусклости», «вогнутости» и прочие искривления поверхности. По внешнему виду кристалла также можно судить о происходящем (или планируемом) процессе, но для того, чтобы делать подобные выводы, потребуется накопить статистику в построении подобных моделей, а затем, классифицировать наиболее типичные случаи. Такая работа может быть проведена в будущем.
Итак, в данной статье я попытался изложить методику планирования с помощью объемных моделей на уровне идей. Постарался показать, что переход к объемным моделям – это вполне закономерное развитие существующей системы планирования согласно законам развития систем. Безусловно, мое видение – это первое приближение, которое впоследствии должно уточняться, дополняться математическим аппаратом. Затем потребуется внедрение. Понятно, что подобные модели могут быть востребованы бизнесом только в том случае, если будут воплощены в виде качественного программного обеспечения и соответствующей коммерческой поддержкой, доступных только крупным софтверинговым компаниям. Так что теперь дело за математическим описанием и последующим внедрением.
Также было бы несправедливо не упомянуть в данной статье Володина Павла, который сделал предположение о возможности описания процесса развития отношений компании продавца и компании клиента в рамках работы над проектами с помощью объемной модели кристалла. Собственно говоря, высказанная им идея и дала мне импульс для разработки основных положений модели планирования, которую я представил в данной статье.
Статья опубликована в журнале «Новости менеджмента«, №2 (32) 2013 г.
